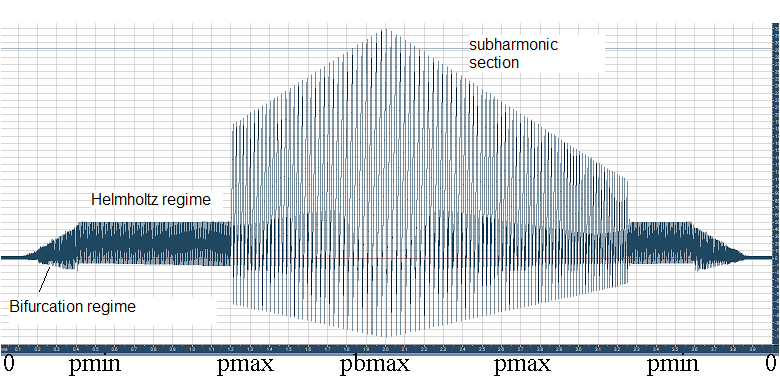
The violin bow-string interaction is a self-organizing sytsem. It can have several regimes. The regular Helmholtz or sawtooth motion is reached when the bowing pressure is medium. When the bowing pressure is increased, beyond a certain threshold suddenly the pitch changes dramtically. It is getting much lower. From then on the pitch of the violin is determined no longer by the fingering on the fretboard but by the bowing pressure itself. It takes more bowing pressure to get into this subharmonic regime than it takes to leave it, the system has a hysteresis. When the bowing pressure is lowered from the regular Helmholtz regime, again suddenly the sawtooth motion breaks down and goes into a bifurcation regime with many periodicities possible.
In the figure below a Finite-Difference Time Domain (FDTD) model of a bowed string is driven through in- and decreasing bowing pressure. The correlogram below shows the regime changes:

During regular Helmholtz motion, when the string tears-off the bow two waves or impulses are leaving the bowing point into the two directions, towards the bridge and towards the nut. Both are reflected at bridge/nut and return to the bowing point. Only the second is strong enough to tear-off the bow from the string. This second impulse has travelled the whole distance of the string twice. Therefore the periodicity of the sawtooth motion is determined by the finger position on the fretboard.
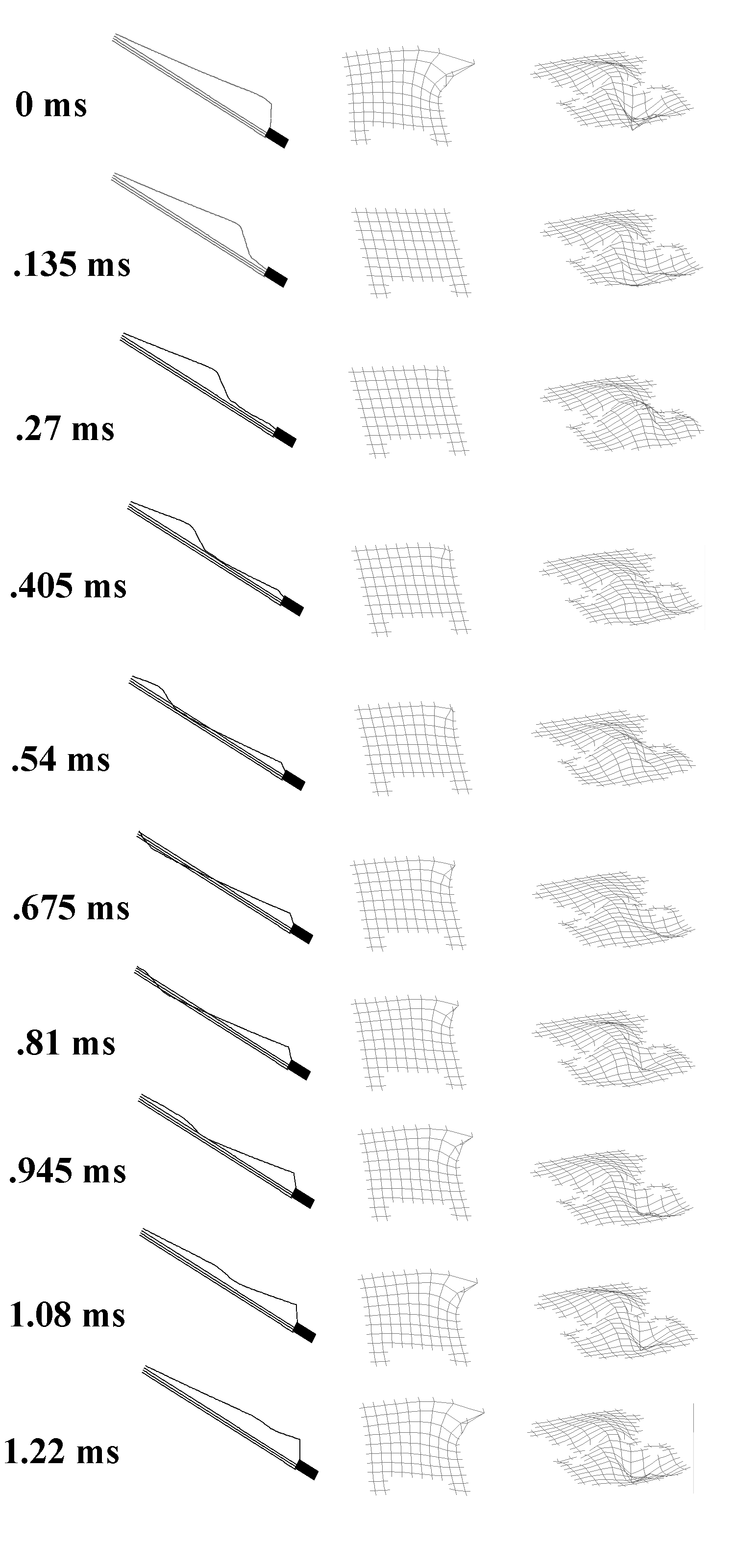
The string displaces the violin bridge, which is very stiff with a fundamental frequency of about 2.5 kHz. Therefore the violin sound is loudest at this frequency, the so-called ‘bridge hill’. The bridge more or less transfers the violin bow displacement to the violin top plate without mit damping, as the bridge is so stiff. The violin top plate is then displaced mainly in a distorted dipole mode, as the bridge has too feet. Still as the soundpost is stiffening the violin body the dipole is more transfered into a monopole, which is much louder in radiation. Below is the displacement of the violin bow, bridge, and top plate for one cycle of a played note: