When blowing into a saxophone mouthpiece with flow in the mouthpiece becomes turbulent forming a vortex or eddy. Below is a video showing this:
Video_1_Saxophone_Mouthpiece_Reed_A 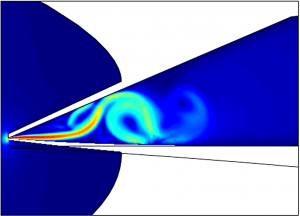
The video is an excerpt, the whole geometry looks like this:
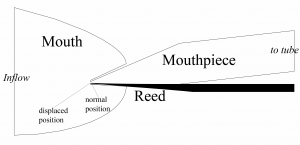
This vortex forms a pressure impulse which travels down the tube, is reflected at the horn and comes back to the mouthpiece. There it triggers the reed to move. This movement opens (or closes) the small slit between the reed and the mouthpiece and the air flowing into the mouthpiece changes again. This leads to a reformation of the vortex and another pressure impulse is produced which again travels down the tube. Therefore the length of the tube determines how the played pitch is.
The interesting thing is that the impulse traveling down the tube is heavily distorted, by the horn, by open finger holes, valves, etc. But then the saxophone sound would need to have no longer harmonic overtones as then for each frequency the tube would have a different length. Still the saxophone sound has perfectly harmoic overtones. The reason can be seen in the video above. The impulse coming back to the reed might be distorted. Still this does not matter as it only triggers the reed to move again. Then the air flow into the mouthpiece is producing another impulse which looks perfectly the same as the previous one when it started. Therefore all impulses look the same and we hear a harmonic overtone spectrum.
This is a self-organizing process due to the heavy nonlinearity of the turbulence. Still only because of this heavy nonlinearity the system is able to orgnize itself, to result in a very simple output, in the harmonic overtone spectrum. Therefore reed instruments are self-orgnaized systems.
Saxophones also have a formant region around 3 kHz. There the sound of each note is loud, no matter which note it played. Such a frequency region, one which is loud independent from the played pitch, is called a formant region. This is also known from the voice, where normally two such strong regions lead to the formation of the vowels ‘a’, ‘e’. ‘i’, etc.
Different reeds are known to produce different sounds. When inserting the above physical model four different reeds which slightly different goemtry as used by Vandooren
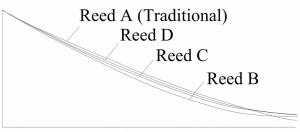
then the reed tip is moving differently with each reed. One can see that the periodicity of the reed depends on the pitch of the saxophone. Still after it was triggered it moves for itself a bit. This movement has a frequency of about 3 kHz producing the enhanced aplitudes of the saxophone sound there. And as this movement is independent form the pitch played it is a formant region.
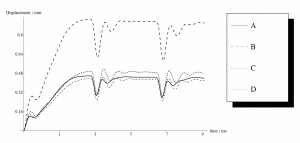
Making a Fourier-Analysis of this time-series we find that the spectrum around 3 kHz is more or less strong for the different reeds:
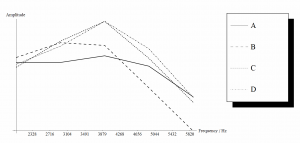
Then the reed with the strongest formant is more ‘Jazzy’, while the one with the least is more ‘Classical’ (at least according to Vandooren). So speaking with a saxophone is more easy with the Jazz-reed as it already has a formant region, like the human voice has.
Lit.:
Bader, R.: Individual reed characteristics due to changed damping using coupled flow-structure and time-dependent geometry changing Finite-Element calculation. In: Forum Acusticum joined with American Acoustical Society Paris 08, 3405-3410, 2008.
Bader, R..: Nonlinearities and Synchronization in Musical Acoustics and Music Psychology. Springer Series Current Research in Systematic Musicology, Vol. 2, Springer Heidelberg , 2013.
