Physical Modeling of musical instruments is taken the geometry of the instrument and its material parameter and solving the differential equation governing its vibrations.
When looking at the eigenmodes the instrument vibrates in. the result are pictures of these vibrational modes as well as the frequencies it vibrates in. When calculating the model time-dependent the result is a sound of the instrument.
Basically there are two types of such models used with musical instrumens, Finite-Difference Methods (FDM) and Finite-Element Methods (FEM). With FDM the geometry is represented using many points for which the equations are solved. Here is a grid of a guitar top plate using FDM (see guitar page of more details for this model):
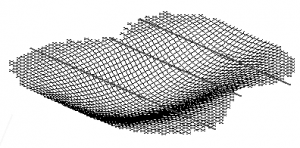
When using FEM the geometry is assumed to consist of many small elements, most often triangles or tetraeders. ABalinese Metallophone Gender dasa:

consists of bronze plates like this:

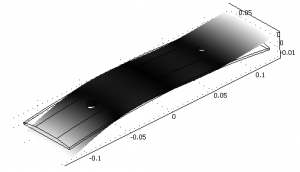
This can be discretisized as FEM mesh like:
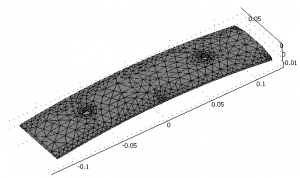
From this mesh eigenmodes, the modes of vibration can be calculated, e.g.:
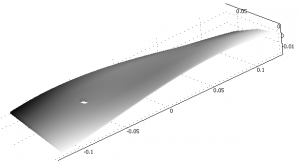
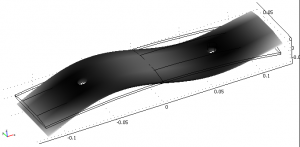
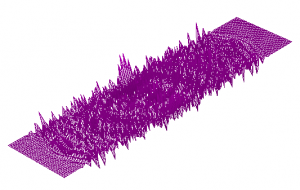
Using a FDM model the plate can be struck and a time-dependent simulation can be performed. Here is a snapshot of the vibration very shortly after the strike:
With the gender the question was where the great brightness of the sound comes from. Modeling the plate with the trapezoid shape and without it it clearly appears that the trapezoid shape is causing the trapezoid shape.
The gender with trapezoid shape:
And here the flate shape:
The above sounds are with a free plate. When fixing it at the two points where it is fixed in reality the sounds change their pitch a bit, but the brightness stays the same. Again the trapezoid shape:
and the flate one:
Lit.:
Bader, R. (ed.): Springer Handbook of Systematic Musicology. Springer, Heidelbert 2018.
Bader, R..: Nonlinearities and Synchronization in Musical Acoustics and Music Psychology. Springer Series Current Research in Systematic Musicology, Vol. 2, Springer Heidelberg , 2013.
Pfeifle, F., Bader, R.: Real-Time Finite-Difference Method Physical Modeling of Musical Instruments Using Field-Programmable Gate Array Hardware, J. Audio Engineering Society 63 (12), 1001-1016, 2015.
Bader, R.: Additional modes in a Balinese gender plate due to its trapezoid shape. In: Bader, R., Neuhaus, Ch, & Morgenstern, U. (eds.): Concepts, Experiments, and Fieldwork: Studies in Systematic Musicology. Peter Lang Verlag, Frankfurt a.M. 95-112, 2009.
Pfeifle, F. & Bader, R.: Real-Time Physical Modelling of a real Banjo geometry using FPGA hardware technology. In: Bader, R. (ed. / Hrsg.).: Musical Acoustics, Neurocognition and Psychology of Music / Musikalische Akustik, Neurokognition und Musikpsychologie. Hamburger Jahrbuch für Musikwissenschaft 25, 71-86, 2009.
Bader, R. & Hansen, U.: Acoustical Analysis and Modeling of Musical Instruments Using Modern Signal Processing Methods. In: Handbook of Signal Processing in Acoustics. D. Havelock, M. Vorländer, S. Kuwano (ed.). Springer, 219-247, 2008.
Bader, R.: Whole geometry Finite-Difference modeling of the violin. In: Proceedings of the Forum Acusticum 2005, 629-634, 2005.
Bader, R.: Physical model of a complete classical guitar body. In: Proceedings of the Stockholm Music Acoustics Conference 2003, R. Bresin (ed.) Vol. 1, 21-124, 2003.
