The pitch theory explains how pitch is heard in the auditory pathway, as the massive presence of the fundamental periodicity at all auditory Bark bands.
Still how does pitch perception work when two instrumnets play at the same time, or when one instruments plays chords? From musical training we konw how hard it can be to identify an interval of two tones e.g. played on a piano. We also know from musical instruments we are not used to, like those from other ethnic groups, that it even is hard to say if there is one pitch, or two, or even more than two.
In these cases the souind might be fused, the two or more tones might sound not very separate. In a listening test this separateness was asked for. The 30 sounds used were 13 guitar and 2 piano and a synth pad sounds, familiar to the Western listening subject, all other sounds were from non-Western instruments like the Cambodian metallophone roneat deik, the Chinese reed-instrument hulusi, a Uyghur two-stringed dutar, a mbira thumb piano, or Myanmar gongs. The 13 guitar sounds had all 13 intervals in one octave, unisono, minor second, major second, minor third, etc. to octave.
Now we would expect the familar guitar intervals sound much more separate to listeners, as they know these sounds.
Additionally, a well-known parameter, the roughness of the sounds was asked for. This gives a glue for the difference between roughness and separateness.
Here is the result for both, the separateness (yellow) and roughness (blue) for all 13 guitar intervals (left: unisono, right: octave):
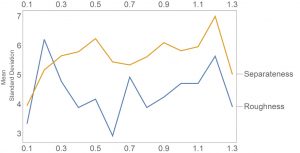
The roughness goes as expected. Unisono and octave are low in roughness. Fifth and fourth are too, all other intervals have larger roughness. Of course a minor third sounds much more rough than a fifth.
The separateness is different. Above the fifth, on the right side of the plot, separateness and roughness more or less align. Still below the fifth they are going about opposite. So roughness and separateness are two different parameters. If two pitches are close togeter they sound more fused, if they are further apart they sound more separate. This might sound expected, still e.g. the major 7th is astonishing. This interval is rough, still perceived very separate.
As we now have an idea how this works we can compare the familiar and the unfamiliar sounds. Below is again the roughness curve for the guitar, but now all other sounds are added:
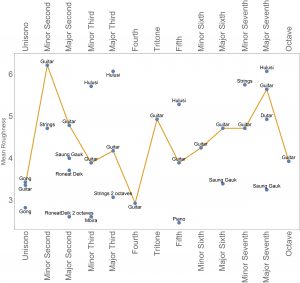
We see that for low intervals (minor second, major second) all non-familiar sounds are perceived much less rough than the guitar sounds. This no longer holds for the higher intervals.
Still more surprising is the perception for separateness:
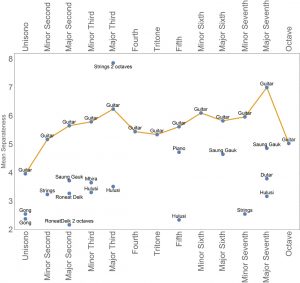
Nearly all unfamiliar sounds are below the guitar sounds! One exception is a string pad sound, which is an interval with two octaves in between. Here indeed everybody immediately hears them separate.
This makes us conclude that when sounds are familiar their auditory perception is different. Known and learned sounds are identified as having two pitches, therefore need to sound more separate than unfamiliar sounds, where one is not even sure if there are one or many pitches.
To decide about how and where in the brain these mechanisms might be placed we need the cochlear model and the pitch theory.
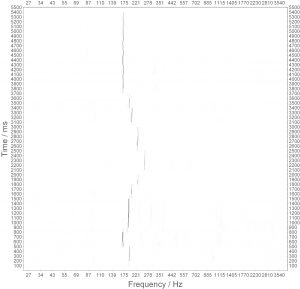
A melody played by a single saxophone is represented in the auditory system right according to the pitch theory. Below time is up, so following the melodie means going from bottom to top:
Things get more complex when two tones are played at the same time, here a guitar playing the interval D-F:
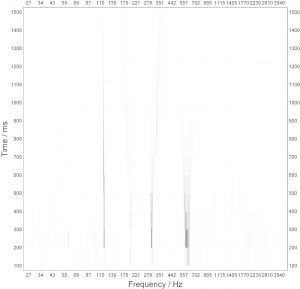
We expect two strong lines, instead there are three, the fundamentals of the two pitches and a residual pitch.
Or how about an arpaggio of a C-Major chord played by a piano:
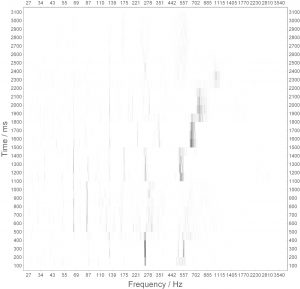
Clearly the arpaggion is there, still there are many other lines coming with it.
In a way, the plots above represent the sound perception, as pitch is there, but much harder to follow compared to a single-line melody.
So how is the auditory system processing multi-pitch sounds. It is interesting to investigate this in terms of roughness using synthesized sounds of two tones playing simultaneously, each consisting of 10 harmonic partials. Calculating all possible combinations of two-pitches within an octave in 1 Cent steps we can do statistics on the results.
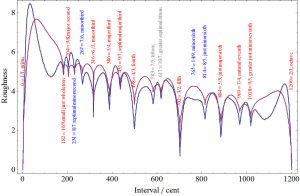
At first we calculate the roughness according to the Helmholtz/Bader and the Sethares algorithm for the sounds. As expected the roughness is least for the harmonic intervals and much more for more complex ones. So we know the sounds are ok:
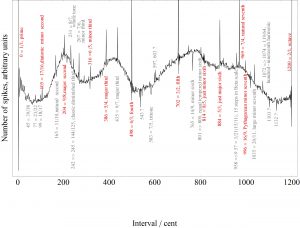
Now for the cochlear model. Below the number of spikes are shown for all intervals within an octave. The harmonic relations, fifth, fourth, thirds, sixth, all have a very sharp peak, where much more spikes are produced compared with the other intervals:
We can also calculate the entropy of the cochlear model output spike train, how much it is diffused. Strongly diffused patterns have a high entropy, patterns which show simple, clear peaks have low ones: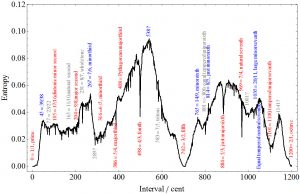
Again this works with the major intervals, still very different. The fifth has a large gap instread of a sharp peak. The same holds for the third. Still the fourth is again very sharp.
So now we can compare the results of the listening test and the cochlear model output. The peaks shown above for the saxophone and piano sounds (spikes over frequency and time) need to be further processed. This is done using a peak-detector. Such a detector can be tuned. One can blur the peaks, then we have a kind of integration in time and frequency. This corresponds roughly to a coincidence detection, where spikes are synchronized in further auditory cortex processing. Such coincidence detection is indeed happening. The plots below have the coincidence detection in the up-axis. At the bottom there is no coincidence detection assumed, the higher values have more and more coincidence detection applied.
Also we can choose to use only a few spikes, leaving out the bottom noise. Neurons do produce noise anyway, therefore we might neglect peaks which are too low.
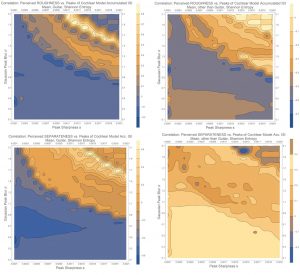
Then we can correlate perception with the cochlear model. Below are four plots, two for roughness (top row) and two for separateness (bottom row). Also the sounds were again split into familiar sounds (the two on the left, the guitar) and unfamiliar (the two on the right, all the rest).
There is a line from right bottom to left top. This is expected, when no coincidence and strong peak selection (right bottom) is similar to high coincidence detection and low peak selection (left top).
Still the most interesting part is that this line is the opposite for the familiar (left) compared to the unfamiliar (right) plots. With familiar sounds the correlation is negative, while with unfamiliar sounds the correlation is positive.
So if a sound is unfamiliar a high spike entropy is perceived rough, as expected. Still for familiar sounds it is vice versa! Also when a sound is unfamiliar a high spike entropy is perceived as high tone separateness. And again when the sound are familiar the opposite is true:
So we can conclude that there are two different methods of perceiving multi-pitch sounds. With unfamiliar sounds the spikes as present in the auditory pathway are correlating with perception. This is the immediate perception of sound, the experience of sound itself. Still when the sounds are known the processing seems to happen somewhere else, most likely in the cortex. Here musical training seems to come in, the knowledge that sounds consist of several tones, maybe even being able to identify the interval. Still this is not an immediate perception anymore, the focus is on identification and therefore focussed on abstraction.
