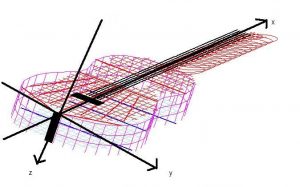
A classical guitar consists of top plate, back plate, ribs, neck, inclosed air and strings. When using a Finite-Difference Time Domain (FDTD) method, the differential equations governing the vibration of the instrument can be solved, the guitar vibrates virtually in a computer:
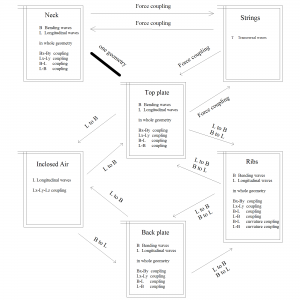
The different guitar parts are connected in a complex way exchanging different kinds of vibrations:
A Digital Guitar Workshop software has been developed to built own guitar geometries and calculate their sounds. It also displays many classical guitars measured in terms of their geometries and their sound radiation.
Plucking a string:
leads to a movement of the top plate
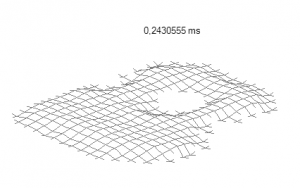
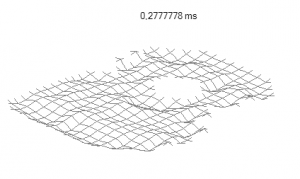
and all other guitar parts in time.
The strings act as impulses to the top plate. The two videos below show a banjo. In the first one can see that the string is at rest for nearly the whole time, only ‘knocking’ on the membrane for a short time span. The second shows that the string is at rest nearly all the time.
The different parts of the guitar contribute different sounds to the whole guitar sound. Below are the radiations of the different guitar parts of the physical guitar model. The top plate comes in immediatelly contributing the tone attack. Still the top plate itself sound rather simple. Still the back plate contributes the lower and the ribs the higher mid frequencies. But they come in slower therefore making the tone ‘slower’ too. The neck contributes hights. The inclosed air is mainly responsible for the low frequencies, including the Helmholtz resonance. Still it comes in only very slow because air has a much lower sound speed compared to wood. So the resulting tone is a combination of all parts leading to a complex guitar sound: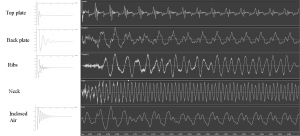
The different parts of the guitar therefore sound very different. Here are some examples of the same piece played on the physical modeling guitar (the strings are brighter than with a real guitar to make the effect more clear):
The top plate along:
The back plate alone:
The ribs alone:
The neck alone:
The inclosed air alone:
All together:
The top plate of a guitar has certain eigenmodes it vibrates in. The model shows these eigenmodes for the lowest frequencies:
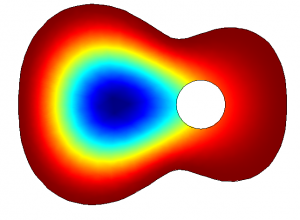
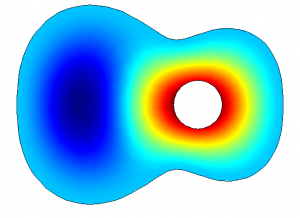
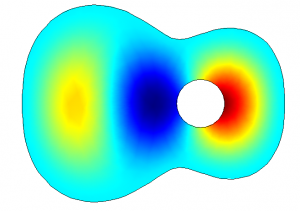
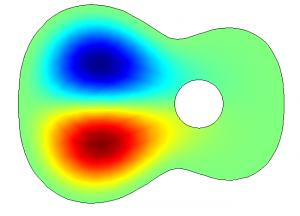
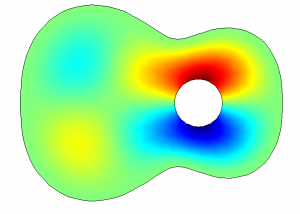
Still when plucking real strings the top plate of the guitar vibrates in a very much different way. Below are the forced oscillation patterns (FOP) of a guitar top plate when plucking the open strings and taking the first five harmonics. The figure is sorted in terms of frequencies, starting with the lowest frequency at the left upper corner. Higher frequencies are along the row and down the columns (all measured with a microphone array):
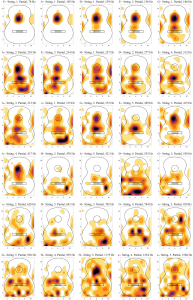
The lowest frequencies nearly only have a radiation from the sound hole. This is the Helmholtz resonance as expected. But then the radiation patterns differ considerably from the ‘theoretical’ modes shown above. The reason is that forcing a plate to vibrate with the frequencies of the string leads to very different vibrations than when letting the plate vibrate on its own. The main reason is internal damping caused by viscoelasticity.
Additionally, a strong driving-point dependency is present. When plucking all six open string (below from left to right, with most left the lowest open E-string) and showing only frequencies aroung 300 Hz. Clearly the forced oscillation pattern has its strongest amplitudes around the impact point of the played string:

This is also found with the piano.
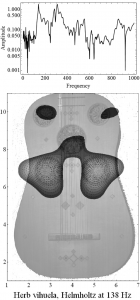
Multiple sound holes are sometimes used, below is an example of a replica of the Guadalupe vihuela, a Spanish Renaissance guitar. It has five sound holes, where radiation is mainly taking place at the sound holes near the middle of the instrument. The reason is that the air inside the instrument has most freedom to vibrate there. The air at the instrument ribs is restricted by the ribs to vibrate freely. Therefore when designing a guitar with several soundholes the radiation strength depends on the placing of the soundholes.
Lit.:
Bader, R.: Computational Mechanics of the Classical Guitar. Springer 2005.
Richter, J., Münster, M., Bader, R.: Calculating guitar sound radiation by forward-propagating measured forced-oscillation patterns, Proc. Mtgs. Acoust. 19, 035002, http://dx.doi.org/10.1121/1.4799461, 2013.
Münster, M., Richter, J., Bader, R.: Eigenvalue shapes compared to forced oscillation patterns of guitars, Proc. Mtgs. Acoust. 19, 035001, http://dx.doi.org/10.1121/1.4799103, 2013.
Bader, R.: Radiation characteristics of multiple and single sound hole vihuelas and a classical guitar. J. Acoust. Soc. Am. 131 (1), 819-828, 2012.
Bader, R.: Characterizing Classical Guitars Using Top Plate Radiation Patterns Measured by a Microphone Array. Acta Acustica united with Acustica 97, 830-839, 2011.
Bader, R.: Reconstruction of radiating sound fields using minimum energy method. J. Acoust. Soc. Am. 127 (1), 300-308, 2010.
Beurmann, A., Bader, R., & Schneider, A.: An acoustical study of a Kirkman harpsichord from 1766. Galpin Society Journal LXIII, 61-72, 2010.
Bader, R.: Characterization of guitars through fractal correlation dimensions of initial transients. In: J. of New Music Research, 35 (4), 323-32, 2008.
