See also: Impulse Pattern Formulation (IPF)

Musical instruments have traveling impulses going through the instrument body. A saxophone or trumpet sends out short pressure impulses from the mouthpiece which are reflected at the tube end, return to the mouthpiece and nonlinearly interact with the reed or players lips. A guitar string acts with short force impulses onto the soundboard, where the soundboard distributes the impulses to the different body parts, reflects them and returns them to the string again.

The interaction between the impulses constitute musical instruments to produce harmonic overtones at all. The impulse returning to a saxophone mouthpiece triggers the next impulse which looks the same as the one before. Although the returned impulse is strongly distorted which would result in an inharmonic overtone spectrum due to frequency dispersion, the nonlinear mechanism in the mouthpiece results in a synchronization of the frequencies, to a harmonic overtone sound.

With stringed instruments the impulse of the string acting on the instrument body is dissipated strongly and therefore does not have the strength to drive the string with the frequencies of the body. Furthermore due to the many reflection points in the instrument body the returning impulses are weak compared to the strong impulse on the string, which is only one-dimensional and therefore keeps the impulse energy together. Therfore the string forces the body to go with the strings frequencies, as the string is less damped and lower in dimensionality compared to the body.

The returning impulses might be regular as with a harmonic sound. Still they can become quite chaotic during initial transients, multiphonic sounds with bifurcations or in subharmonic or biphonations with the singing voice.

The Impulse Pattern Formulation (IPF) is a top-down method to calculate this impulse pattern acting in musical instruments. It takes a standpoint, say the top plate of a guitar, which distributes the impulse to other parts, which again reflect the impulse returning it at different time points with different strength. The IPF can take any standpoint, the string, the ribs, the back plate, etc.

The IPF can deal with one, several, or very many reflection points. With one reflection point the whole bifurcation and chaotic regimes appear:

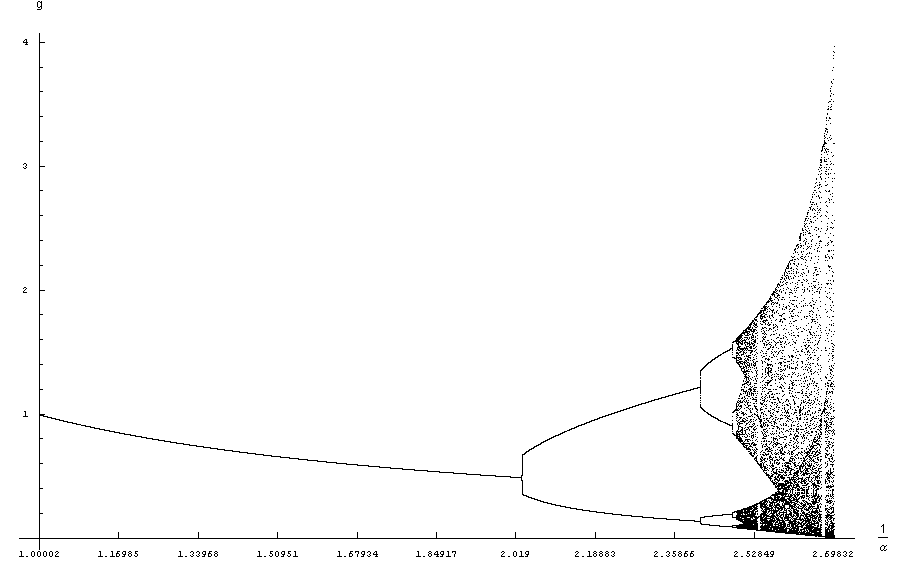
With two reflection points very complex patterns might be present:

So for the example of a guitar the IPFs of the different body parts can be calculated during the initial transient phase of a guitar tone. Comparing this to the initial transient time series of a Finite-Difference Time Domain (FDTD) calculation of a whole guitar body, the phenotype of the transients for the different parts clearly appear:

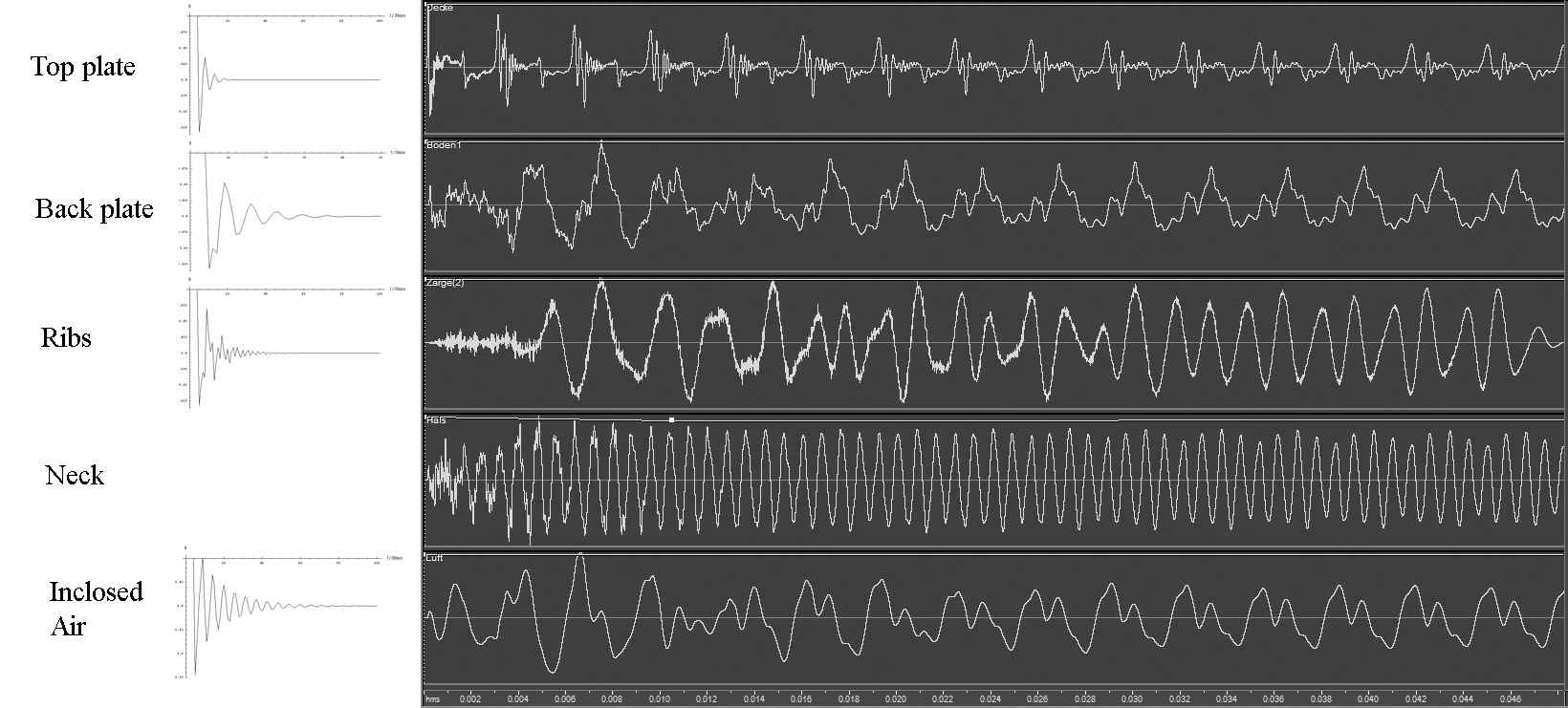
On the right are the FDTD time series of the different plates, on the left are the IPFs.

So e.g. the top plate comes in immediately, indeed it is the part with the hardest attack, while the inside air only converges slowly to its steady state. When a steady tone is reached the IPF does not change anymore, resulting in a horizontal line.

The IPF can be used to synthesize musical sounds easily by adding any waveform shape between two impulses. Here is the initial transient of a trumpet with amplitude raise and a spitting at the tone onset:

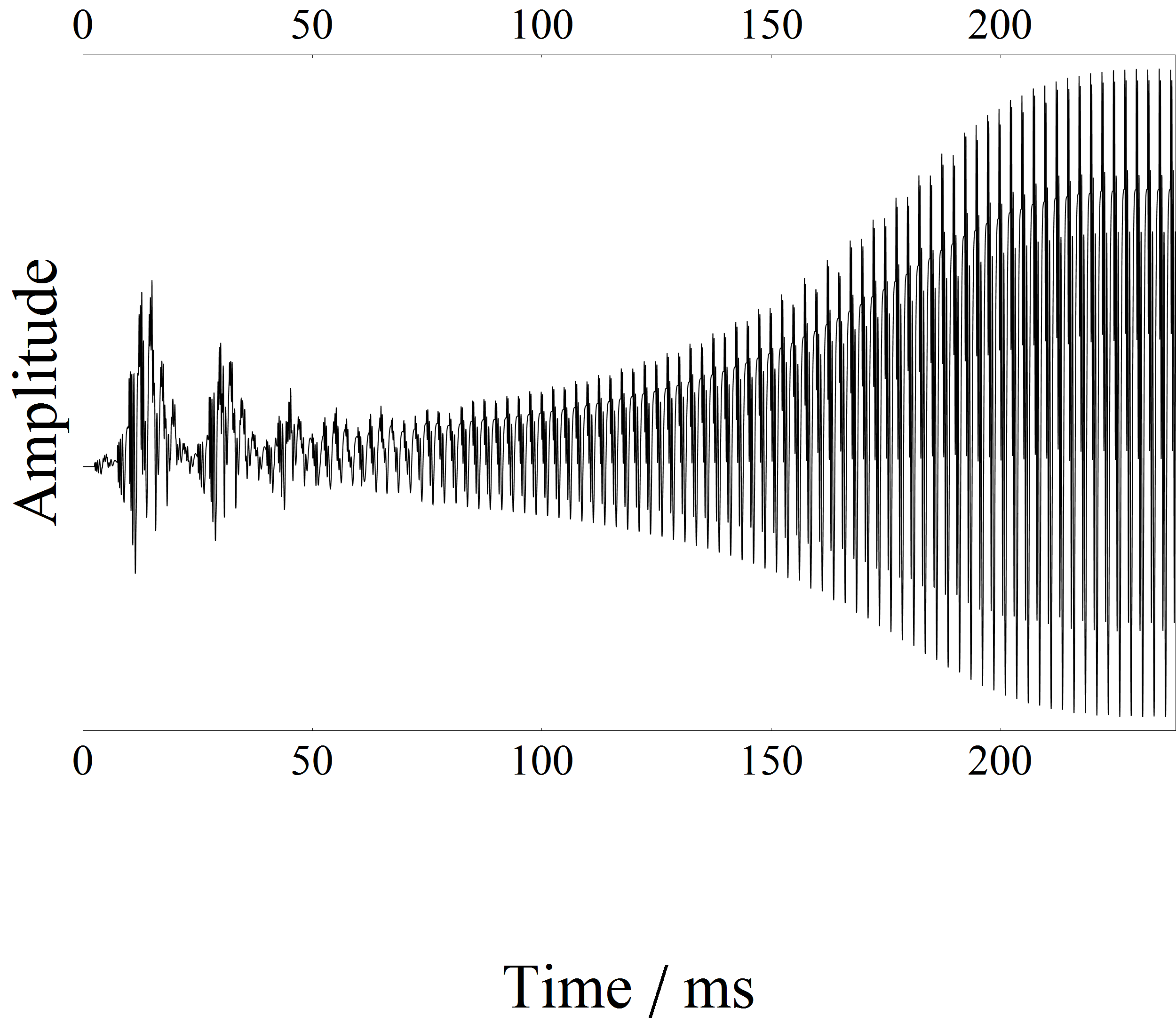
The IPF might also be able to model brain dynamics, as also the brain consists of impulses, the neural spikes. Indeed coincidence detection in the auditory nerve tries to reconstruct the IPF of musical instruments, as the IPF acting in the instrument is blurred through reverberation in rooms or the nonlinear distortion of the human ear.

Lit.:

Bader, R., Linke, S. & Gernert, S.: Nonlinear Impulse Pattern Formulation dynamical social and political prediction algorithm for city planning and public participation. arXiv:submit/5507296 [nlin.AO] 1 Apr 2024

Sawicki, J., Berner, R., Loos, S.A.M., Anvari, M., Bader, R., Barfuss, W., Botta, B., Brede, N., Franović, I., Gauthier, D.J., Goldt, S., Hajizadeh, A., Hövel, Ph., Karin, O., Lorenz-Spreen, Ph.,Miehl, Ch., Mölter, J., Olmi, S., Schöll, E., Seif, A., Tass, E.A., Volpe, G., Yanchuk, S. & Kurths, J.: Perspectives on adaptive dynamical systems. Chaos 33, 071501 (2023) https://doi.org/10.1063/5.0147231

Bader, R.: Modeling Temporal Lobe Epilepsy during Music Large-Scale Form Perception Using the Impulse Pattern Formulation (IPF) Brain Model. Electronics 13(2), 362, 2024. https://doi.org/10.3390/electronics13020362

Bader, R.: Impulse Pattern Formulation (IPF) Brain Model. arXiv:2212.11021, 2022

Bader, R..: Nonlinearities and Synchronization in Musical Acoustics and Music Psychology. Springer Series Current Research in Systematic Musicology, Vol. 2, Springer Heidelberg , 2013.

Linke, S., Bader, R. & Mores, R.: The impulse pattern formulation (IPF) as a model of musical instruments—Investigation of stability and limits, Chaos 29, 103109-1, 2019.

Linke, S., Bader, R. & Mores, R.: Describing minimum bow force using Impulse Pattern Formulation (IPF) – an empirical validation. POMA 2022.

Linke, S., Bader, R., & Mores, R.: Modeling synchronization in human musical rhythms using Impulse Pattern Formulation (IPF). arXiv:2112.03218, 2021

Linke, S., Bader, R., & Mores, R.: Influence of the supporting table on initial transients of the fretted zither: An impulse pattern formulation model. Proc. Mtgs. Acoust. 43, 035003 (2021); doi: 10.1121/2.0001494

Linke, S., Bader, R. & Mores, R.:The Impuls Pattern Formulation (IPF) as a nonlinear model of musical instruments. Proceedings International Symposium of Musical Instruments (ISMA), 1-10, 2019.

New: the fretted zither and the electric guitar

Modern fretted zithers come in two acoustic types: some behave more like a harpsichord, others more like a grand piano. Measurements of several instruments show where these differences come from in the construction. In electric guitars, the magnet of the pickup pulls on the strings: the closer it sits, the more it changes how the strings vibrate – and even whether the guitar plays in tune.

New: IPF and rhythm – how musicians synchronise

When musicians play together, they constantly adjust their tempo to each other. We modelled this with the IPF: every beat is an impulse, and the time to the next beat depends on the beats played before. Played against a click track, the IPF reacts to sudden tempo changes much like human players do: it overshoots, swings around the new tempo for a few beats and then locks in, usually within fewer than ten beats. Very large jumps may be ignored, or the IPF switches to double time. Slow, continuous tempo changes are followed closely, with a small delay of about an eighth note – musicians also lag slightly behind. Therefore, the IPF can be used as a rhythmic partner that plays along with musicians in real time.

Linke, S., Bader, R. & Mores, R.: Modeling synchronization in human musical rhythms using Impulse Pattern Formulation (IPF). arXiv:2112.03218, 2021.

New: the IPF brain model

The brain also works with impulses: neural spikes and bursts are sent out from one region, reflected by others and return delayed and damped. The IPF brain model treats these neural reflection points just like the parts of a musical instrument. It is computationally very cheap and still behaves realistically. With 10–20 % inhibitory neurons, as found in the real brain, it adapts best to an outside stimulus. Its strongest reflections appear at delays around 300 ms, the time scale of event-related potentials measured with EEG. And it settles within about five seconds, the time scale of short-term memory.

To let the model listen to music, a physical model of the cochlea is put in front of it. Listening to the piece “One Mic” by Nas, the brain model synchronises most strongly in the gamma band around 50 Hz and follows the loudness and tension of the music – as found in EEG experiments. During quiet passages with a steady rhythm, however, the whole network synchronises. Such a state corresponds to temporal lobe epilepsy, which is associated with trance, creativity and spiritual experience.

Coupled with an IPF model of the larynx, the brain model has become a sound synthesis method that plays along with musicians (see below).

New: IPF as a co-musician

An IPF brain model, driven by a simple IPF of sensory input and acting on an IPF larynx model, produces timbre, rhythm, articulation and large-scale form with a single algorithm – a sound-synthesis method that can play along with musicians.

Beyond music: social and political prediction

The IPF also predicts social and political developments. In a city-planning model, each stakeholder – artists, residents, investors, the city – is one interacting, self-adapting part, and the model shows when a planning process converges, oscillates or breaks down. More on the page Social/Political Prediction IPF and in the interactive Hexenwäldchen.

Literature

Linke, S., Fiegl, J. G., Kontopidis, P., Bader, R. & Mores, R.: Between harpsichord and grand piano paradigms – Acoustical differences of modern fretted zithers. J. Acoust. Soc. Am. 157, A310, 2025.

Linke, S., Kuchenbecker, P., Mores, R. & Bader, R.: The influence of single-coil pickup height on string vibration and intonation in electric guitars. 2025.

Bader, R.: Impulse Pattern Formulation (IPF) Brain and Larynx Model as a Co-Musician Sound Synthesis Method. Proceedings ICMC 2026.

Bader, R., Linke, S. & Gernert, S.: Nonlinear dynamical social and political prediction algorithm for city planning and public participation using the impulse pattern formulation. Chaos 34, 093130, 2024.